在科技日新月异的今天,无损检测技术以其独特的优势,在工业生产、科学研究及医疗诊断等领域发挥着不可替代的作用。其中,超声检测作为一种重要的无损检测方法,凭借其高精度、非破坏性、适用性强等特点,成为检测材料内部缺陷、评估结构完整性的首选工具。本文将带您深入探索超声检测背后的科学原理,特别是那些至关重要的公式,以及它们如何在实践中大显身手。
超声检测的基本原理
超声检测的核心在于利用超声波(频率高于20kHz的声波)与被检测物体相互作用时的物理现象,来推断物体的内部结构和性质。超声波在材料中传播时,遇到不同的介质界面(如缺陷、分层、材质变化等)会发生反射、折射、散射等现象。通过分析这些返回的声波信号,检测人员可以判断物体的内部是否存在缺陷,以及缺陷的位置、大小和性质。

超声检测的关键公式
1. 声速公式
声速(v)是超声波在特定介质中传播的速度,它与介质的密度(ρ)和弹性模量(E)有关,通常表示为:
[ v = \sqrt{\frac{E}{\rho}} ]
对于液体和气体,更常用的是与介质体积模量(K)和密度(ρ)相关的表达式:
[ v = \sqrt{\frac{K}{\rho}} ]
了解声速是超声检测的基础,它直接影响到检测的分辨率和准确性。
2. 反射定律与折射定律
当超声波遇到介质界面时,其传播方向会发生改变,遵循几何光学中的反射定律和折射定律。反射定律表明,入射角等于反射角;而折射定律(斯涅尔定律)则描述了入射波、反射波和折射波之间的速度比与角度关系:
[ \frac{\sin(\theta_1)}{v_1} = \frac{\sin(\theta_2)}{v_2} ]
其中,θ1和θ2分别是入射角和折射角,v1和v2分别是两种介质中的声速。
3. 声波衰减公式
声波在传播过程中会因散射、吸收等原因逐渐减弱,这种现象称为衰减。衰减系数(α)与频率(f)、材料特性及传播距离(x)相关,可用以下公式表示:
[ I = I_0 \cdot e^{-\alpha x} ]
其中,I为传播x距离后的声波强度,I0为初始声波强度。衰减分析对于判断材料的质量和内部结构的均匀性至关重要。
超声检测的应用实例
- 金属材料检测:利用超声波检测金属部件的裂纹、夹杂物、腐蚀等缺陷,确保航空航天、汽车制造等领域的安全。
- 混凝土结构评估:通过测量超声波在混凝土中的传播时间和速度变化,判断结构的完整性,应用于桥梁、大坝等大型工程。
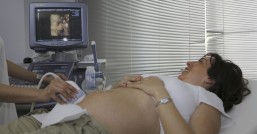
- 医疗诊断:超声波成像技术广泛应用于人体内部器官的检查,如孕期胎儿检查、心脏疾病诊断等,因其无创、无辐射的特点而备受欢迎。
超声检测技术的发展趋势
随着人工智能、大数据等技术的融合,超声检测技术正朝着更高精度、更智能化方向发展。自动扫描系统、三维成像技术以及数据分析软件的应用,极大地提高了检测效率和准确性,使得超声检测在更多领域展现出广阔的应用前景。
结语
超声检测作为一门融合了物理学、材料科学和工程技术的交叉学科,其公式的运用不仅是理论研究的基石,更是实践应用的指南。通过不断探索和创新,超声检测技术将继续在保障产品质量、促进科技进步和维护人类健康方面发挥重要作用。未来,随着技术的不断演进,我们有理由相信,超声检测将开启更多未知领域的探索之门。





发表评论